It has been very common to consider that market prices, and even the application of widely accepted ‘fair’ asset valuation methods, are sufficient to comply with the arm's-length principle. However, this is not necessarily the case, as there are economic phenomena such as synergies that have peculiar implications.
Synergies imply that the interaction of assets, which can occur due to the coincidence of their presence in the same organisation, leads to a joint generation of value greater than the sum of the value generated by each asset individually without interacting with each other.
In terms of an asset transaction, this could mean that the value contribution to the entity buying the asset would not be the same as the amount lost by the entity selling the asset.
Regarding the valuation of the asset in question, a widely accepted path is that of the present value of discounted future cash flows. Here, the main problem is the identification of the company's profits that would be attributable to the asset under analysis.
To simplify this point, the Shapley value tool can help us determine the profits that would be ‘fairly’ attributable to a specific asset located in a company.
The Shapley value
The Shapley value is a wealth distribution method in cooperative game theory under the assumption that everyone collaborates in a large coalition. It is a ‘fair’ distribution in the sense that it is the only distribution with certain desirable properties (efficiency, skewness, linearity, and null player).
Given a group N (of n players) and a function υ∶ 2N → R with υ(∅)=0, where ∅ denotes the empty set. The function v that assigns subsets of real players is called a characteristic function.
The function v has the following meaning: if S is a coalition of players, then v(S), called the value of the coalition S, describes the total sum of the payments to the members of S that can be obtained for such cooperation.
According to the Shapley value, the amount that player i obtains during a coalition game (v,N) is:
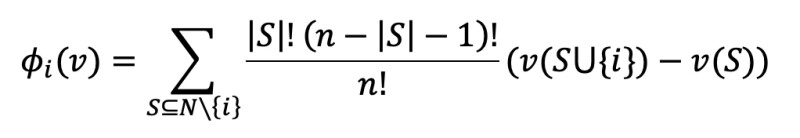
Where n is the total number of players and the sum is spread over all subsets of N that do not contain player i.
An example:
Suppose we have 3 players ({a,b,Δ}), where a is the set of assets housed in A (except Δ) and b is the set of assets housed in B, while Δ is a hard-to-value asset.
Initially, asset Δ is owned by A and its sale to B is analysed. Therefore, the estimate of the ‘fair’ profit corresponding to asset Δ is:
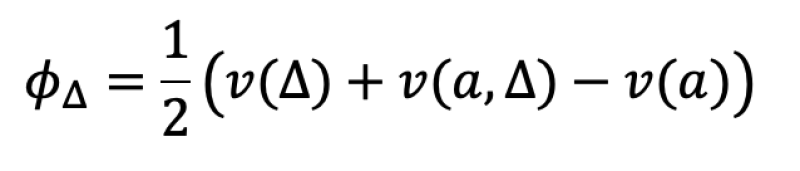
Here, the following is true: f(ϕ)=w,f:R→R where ϕ is the annual utility of an asset and w is the present value of the asset.
The asset price Δ would then be: f(ϕΔ ) = wΔ
Arm's-length implications
In the case above, A should not be willing to sell asset Δ at a price less than f(v(a,Δ)-v(a)), because it would otherwise not compensate for the loss of profits for A from ceasing to exploit asset Δ.
So, assuming the condition v(Δ < v(a,Δ) - v(a) was fulfilled, there would be no impediment for this to occur. Here, wΔ would not be arm's-length despite being a ‘fair’ price, because it is not a price for which the asset owner would be willing to sell.
Furthermore, in the event that the condition v(a,Δ) - v(a) > v(b,Δ) - v(b) was fulfilled, the contract curve between A y B would be ∅. In other words, there would be no possible price at which the transaction would take place, since at any price, either A, B, or both would worsen their initial situation, which would not comply with the arm's-length principle.
What has been described above leads us to reflect that, although the priority of the transfer pricing framework is arm's-length compliance, it may be common that the lack of information in the analysis entails the risk of having no way of demonstrating the existence or finding arm's-length prices.
However, in the same way, market prices as well as theoretical ‘fair’ prices can be an acceptable alternative, especially for the practice of TP analysis.
José Augusto Chamorro Gómez
Senior economist, QCG Transfer Pricing Practice












